Here is a cool documentary on Claude Shannon. As I became familiar with Shannon’s work, I always got the feeling that generally speaking he is an underrated figure and his contributions and influence are deserving of more acknowledgement.
Including Philosophy and/of Information, Logic and Epistemology
Here is a cool documentary on Claude Shannon. As I became familiar with Shannon’s work, I always got the feeling that generally speaking he is an underrated figure and his contributions and influence are deserving of more acknowledgement.
There is too much to read! The journal Metaphilosophy has just made available Volume 41 Issue 3, a special issue on Luciano Floridi and the philosophy of information.
‘Information’ can mean many things. As someone working within the philosophy of information, I have (and sometimes argue for) my select uses of the term. Nonetheless, the term is undoubtedly attached to a range of phenomena. A nice summary of this fact is found in the Wikipedia entry on information:
Information as a concept has many meanings. The concept of information is closely related to notions of constraint, communication, control, data, form, instruction, knowledge, meaning, mental stimulus, pattern, perception, and representation. In its most restricted technical meaning, information is an ordered sequence of symbols.
Continue reading “The Meaning and Etymology of ‘Information’”
Just noticed a significant and potentially confusion causing error regarding multiply modal logics in this nonetheless excellent text. On pages 217-218 in my 1996 edition Hughes and Cresswell write:
For instance we might have a necessity operator
, say, which is stronger than
in the sense that
. The canonical model for such a system would obey the restriction that for all
if
then
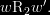
Now, that should be for all 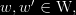 if
if 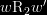 then
then 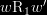 .
.
In this philosophy bites talk Luciano Floridi argues how new technology has changed our relationship to one another and to the world and how this calls for a shakeup in philosophy.
Click here to head over to the talk page.
I also just came across this video of a talk that Floridi gave on the matter:
Professorial Lecture – The Fourth Revolution: The impact of Information Technology on our lives
Who are we? And what is our role in the universe? IT is radically changing not only how we deal with the world and make sense of it, or interact with each other, but also how we look at ourselves and understand our own existence and responsibilities.
If one believes that they believe that p, then do they believe that p (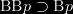 )?
)?
I was recently thinking about this property and its absence from standard systems of doxastic logic. Systems of doxastic logic rightly do not validate the property 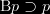 . Since they omit this axiom (commonly called the T axiom),
. Since they omit this axiom (commonly called the T axiom), 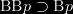 cannot be simply derived. But although the T axiom should not be valid in a doxastic logic, it is fair to say that the axiom
cannot be simply derived. But although the T axiom should not be valid in a doxastic logic, it is fair to say that the axiom 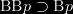 should be valid; if one believes that they believe that p, then they do believe that p.
should be valid; if one believes that they believe that p, then they do believe that p.
This type of agent is apparently termed a stable reasoner by Raymond Smullyan:
A list of doxastic reasoner types can be found here
Now for something with an epistemological and value theoretical flavour, a paper I have been working on titled ‘Knowledge and Its Value: Some Suggestions as To Why Knowledge Is More Valuable Than True Belief’
I have just come across a paper by Christian Piller titled ‘Valuing Knowledge: A Deontological Approach’, which explores my last idea in depth.
Are contradictions informative? Should they be assigned a non-zero, positive informativeness measure?
One option is to simply say no and assign contradictions a predefined informativeness of 0. This is the line Floridi takes with his theory of strongly semantic information.
Continue reading “Are Contradictions Informative?”