If one believes that they believe that p, then do they believe that p (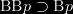
)?
I was recently thinking about this property and its absence from standard systems of doxastic logic. Systems of doxastic logic rightly do not validate the property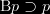 
. Since they omit this axiom (commonly called the T axiom), 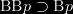cannot be simply derived. But although the T axiom should not be valid in a doxastic logic, it is fair to say that the axiom 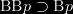should be valid; if one believes that they believe that p, then they do believe that p.
This type of agent is apparently termed a stable reasoner by Raymond Smullyan:
A list of doxastic reasoner types can be found here