What are the properties of information flow? To establish the terminology with which I will pose properties to consider, I start off with the most basic of properties. If A carries the information that B, then A carries the information that B.
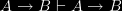
Here are two other straightforward properties of information:
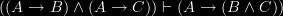

What further properties are there to consider and which should be accepted and which should be rejected in developing an account of information flow?
Well, here are 3 other properties to consider. They are valid in Fred Dretske’s inverse conditional probability account of information flow [see an earlier post here] but come out invalid in standard formal systems for counterfactuals (Jonathan Cohen and Aaron Meskin suggest a counterfactual theory of information).
Property 1, that information flow is transitive, is a property that we would intuitively accept; if A carries the information that B and B carries the information that C, then A carries the information that C. It is a mainstay of Dretske’s account, where it is named the Xerox principle. It is also adopted by Barwise and Seligman in Information Flow: The Logic of Distributed Systems. The transitivity of information flow though has recently been challenged by Hilmi Demir [see http://sites.google.com/site/asilbenhilmi/Demir-Dissertation.pdf?attredirects=0, p. 84.].
What of the other two properties? I would say that Property 2 should be counted as a property of information flow. If A carries the information B, then a unique path can be traced from A back to B. There is a many-to-one relationship between the set X and B, where 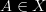 . If
. If 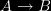 , then every time A obtains B obtains, so if B does not obtain, then neither does A. This principle provokes the realisation that information flows forwards and backwards. Not only can current events carry information about past events, but current events can also carry information about future events.
, then every time A obtains B obtains, so if B does not obtain, then neither does A. This principle provokes the realisation that information flows forwards and backwards. Not only can current events carry information about past events, but current events can also carry information about future events.
As for Property 3, at first I am inclined to say that this also should be counted as a property of information flow. In a strict sense, if A carries the information B, then A should say everything regarding the obtaining of B. Consider this non-monotonic reasoning
- Ellie being a bird carries the information that Ellie flies
- Ellie being a bird and Ellie being an Emu does not carry the information that Ellie flies
In this case, we can simply say that Ellie being a bird does not carry the information that Ellie flies. There is insufficient information to imply that Ellie does or does not fly. However
- Ellie being an emu carries the information that Ellie does not fly
- Ellie being an eagle carries the information that Ellie does fly
So information flow would be monotonic if A carries the information B implies that A is truly a sufficient condition for B. Being a bird is not a sufficient condition for flying. Being a bird does carry information about the probability of flying though.
However, one could take this non-monotonic reasoning further.
- Ellie being an eagle carries the information that Ellie flies
- Ellie being an eagle and Ellie having clipped wings does not carry the information that Ellie flies
An adherence to the monotonicity of information flow would force one to deny the first point here. Only the second point would hold.
But in many of these examples one could just keep on adding extra clauses, so that an apparent information carrying relationship could be invalidated. Perhaps then the best option is to deny the monotonicity of information flow. In the above example, Ellie being an eagle does carry the information that Ellie flies. Maybe one could appeal to something like the Dretskean notion of relevant alternatives in order to accommodate this?
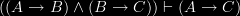
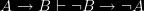
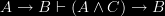
I hope you do not mind my commenting on an older blog post. Regarding non-monotonicity, I think we are indeed in a position where the background conditions for information flow cannot be known, or fully specified, except perhaps within purely mathematical systems.
Jon Barwise and Jerry Seligman tackle this somewhat in their book. Their solution frames monotonicity as valid when reasoning about normal tokens of a local logic. Barwise has a nice paper:
Jon Barwise, “State spaces, local logics, and non-monotonicity,” in Logic, language and computation, vol. 2 (Center for the Study of Language and Information, 1999), 1-20, http://portal.acm.org/citation.cfm?id=330600.