Knowledge and luck do not mix. Our intuitions and definitions of knowledge suggest and require the absence of luck in cases of knowledge. Edmund Gettier’s landmark 1963 paper ‘Is Justified True Belief Knowledge?’ not only prompted a revision in epistemological theorising, but gave us the terms Gettier-examples and the related Gettier-luck. Gettier provided his examples in order to refute the account of knowledge which defines it as justified true belief (JTB). Here is one of the two examples he provided. It is supposed that Smith has strong evidence for the following proposition:
Jones owns a Ford (A)
Smith has another friend, Brown, of whose whereabouts he is totally ignorant. Smith randomly selects the names of three cities and uses them to construct the following three propositions:
- Either Jones owns a Ford, or Brown is in Boston. (B)
- Either Jones owns a Ford, or Brown is in Barcelona. (C)
- Either Jones owns a Ford, or Brown is in Brest-Litovsk. (D)
now, each of B, C and D is entailed by A so Smith comes to accept them. Smith therefore has correctly inferred B, C, and D from a proposition A for which he has strong justification. Hence Smith is justified in having the true beliefs of B, C and D. Now imagine in the scenario that firstly Jones does not own a Ford, but is instead at present driving a rented car. Secondly, by sheer coincidence and unknown to Smith, Barcelona happens to be where Brown is. So even though Smith clearly does not know that C is true, it is true, he believes it and he is justified in believing it.
This example along with the other example in the paper sufficed to show that truth, belief and justification were not sufficient conditions for knowledge. In both of Gettier’s actual examples, the justified true belief came about as the result of entailment from justified false beliefs; in the given example the justified false belief that “Jones owns a Ford”. This led some early responses to Gettier to conclude that the definition of knowledge could be easily adjusted, so that knowledge was justified true belief that depends on no false premises. This “no false premises” solution did not settle the matter however, as more general Gettier-style problems were then constructed or contrived, in which the justified true belief does not result using a chain of reasoning from a justified false belief.
Continue reading “Dretske’s Account of Knowledge Against Some Epistemological Cases”
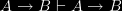
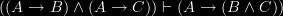

 , including jotting down a sequent system.
, including jotting down a sequent system.